Study Session 15 - Readings 60-65 Fixed Income

Fixed Income

Notes:

• The duration of a floating rate bond is equal to the time until the next coupon payment takes place. As the coupon rate changes semi-annually with the level of the interest rate, a floating rate bond has the same duration as a pure discount bond with time to maturity equal to the time to the next coupon payment of the floating rate bond.
• duration for fixed rate bonds is Duration = Price Yield Down – Price Yield Up / 2 * (initial price) *change in yield in decimals
  

LOS 61a - Explain the risks associated with investing in bonds

Interest rate risk - approximated by measure call duration; when interest rates rise, bonds fall

• Yield Curve Risk - change in shape of yield curve means that yields change by different amounts for bonds with different maturities
  
• Call Risk - risk of issuer calling back the bond, investor must reinvest at a lower rate


• Prepayment Risk - increase in interest rate volatility (like with call risk) causes prepayment; investor must reinvest at lower rate


• Reinvestment Risk - when market rates fall, cash flows (principal and coupon) from bond must be reinvested at lower rate


• NB Investor can be faced with choice between reinvestment risk and price risk e.g. non-callable zero coupon bond has no reinvestment risk (no cash flows to reinvest) but has more interest rate risk than a coupon bond of same maturity) and vice versa


• Credit Risk - if creditworthiness of issuer declines, required return increases, decreasing security's value


• Liquidity Risk - if bond is not very liquid, may have trouble selling it and sell for discount


• Exchange-rate risk e.g. foreigner investing in T-bills will risk relative value of home currency to dollar
  
• Inflation Risk - uncertainty about future purchasing power of cash flows


• Volatility Risk - with embedded options (call/put/prepayment) interest rate volatility affect value of the options and therefore the value of the security


• Event Risk - events outside of the financial market e.g. catastrophe, corporate takeover


• Sovereign Risk - risk of changes in government attitudes and policies toward repayment and servicing of debt; also change in Sovereign's ability to pay, etc.

LOS 61b - Identify the relations among a bond's coupon rate, the yield required by the market, and the bond's price relative to par value (i.e., discount, premium or equal to par)

• Bonds tend to be issued with the coupon rate of similar bonds so they initially trade at par


• they trade at a discount to par when they become more risky (e.g. credit issues with issuer) or less desirable relative to other assets (interest rate rises)


• if required yield falls, bondy trades at a premium

LOS 61c - Explain how features of a bond (e.g. maturity, coupon, and embedded options) and the level of a bond's yield affect the bond's interest rate risk
Interest rate risk = duration = sensitivity of a bond's price to a change in yield (inverse relationship) = similar to elasticity except inverse i.e. bond yield goes up, price goes down

• ceteris paribus longer maturity = higher duration


• ceteris paribus higher coupon rate = lower duration

both of these are intuitive: with longer maturity, you are locked in to a particular coupon until maturity, so the value of your bond will be sensitive to returns on other securities. with higher coupon rate, the percentage different between your coupon and the yields of other investments would be smaller

• callable bond will have lower duration because the upside for the investor is capped at the call price; when interest rates decline, bond price will rise but (almost) never above the call price
  
• putable bond will have lower duration as well because downside for the invest is capped at put price; when interest rates rise, bond price will fall but (alomst) never below put price
  
• This is also intuitive; embedded options limit the price movement of a bond because the privileged part will either put or call the bond at the strike price


• maturity up = interest rate up = higher interest rate sensitivity/duration
  
• coupon up = interest rate down = lower interest rate sensitivity/duration
  
• add a call = interest rate down = lower interest rate sensitivity/duration
  
• add a put = interest rate down = lower interest rate sensitivity/duration

NB remember duration is basically sensitivity to changes in yield

LOS 61d - Indentify the relationship among the price of a callable bond, the price of an option-free bond, and the price of the embedded call option

• call option favours issuer, put option favours bondholder
  
• call option decreases value of bond compared to option-free bond

callable bond = value of option-free bond-value of embedded call option

difference between value of option-free bond and callable bond will be greater at lower yields because price will rise as yield declines but as price gets closer to call price...

LOS 61e - Explain the interest rate risk of a floating-rate security and why such a securities prcie may differ from par value

floating rate is an imperfect insurance against interest rate risk; it is imperfect because the coupon does not float fluidly with market yields but instead is reset at particular dates (and should return to par value).

The longer the reset period the greater the interest rate risk at any reset date; the closer you are to a reset date, the lower the interest rate risk

Coupon resets may not return the bond to par value due if one or both of the following factors are present:

• caps - if interest rates rise above the bond's yield cap, the floating rate security will trade at a discount (cap risk)
  
• fixed margin - e.g. LIBOR plus 2% - the 2% margin reflects liquidity and credit risk of issuer; if these improve, the security will trade at above part; even if firm's creditworthiness remains constant, a chance in the market's required yield premium for the firm's risk level will cause the value of the floater to differ from par

LOS 61f - Computer and interpret the duration and dollar duration of a bond

duration = approximation of the percentage change in security price for a 1% change in yield (so yield is denominator)

• duration = -(% change in bond price/yield change in %)
  
• minus sign because it is an inverse relationship; price goes up, yield goes down
  
• duration of a zero coupon bond will be ~years to maturity;
  
• duration of floater = fraction of a year until the next reset date

NB if you are given the duration, remember inverse relation between price and yield. If you are given a duration of 2 and a yield increase of 5 then you would expect the price to go down by 2*5 = 10% decrease

• percentage price change = -duration * (yield change in %)

dollar duration = approx. price change in dollars in response to a 1% change in yield e.g.with a duration of 5.2 and bond value of $1.2 million, dollar duration is 5.2% * $1.2 million = $62,400 which make sense since duration tells you the movement in price per 1% change in yield

LOS 61g - Describe yield-curve risk and explain why duration does not account for yield-curve risk for a portfolio of bonds

• OK. So a yield curve illustrates the relationship between bond maturity and yield;
  
• the yield curve risk is the changes in the shape of the yield curve that are not captured by the duration
  
• portfolio's duration is just the market-weighted average of the individual bond's durations and will capture parallel shifts in the yield curve i.e. the curve remains the same shape but moves up or down so yields on all maturity lengths are affected equally
  
• non-parallel shifts change the shape of the curve e.g. short maturity bonds have different sensitivities to change in yield than longer ones
  
• to estimate impact of these non-parallel shifts, use key rate durations i.e. measure sensitivity of portfolio's value to changes in yields for specific maturities (or portions of the yield curve)

LOS 61h - Explain the disadvantages of a callable or prepayable security to an investor

This is intuitive, the disadvantages are:

• you cannot benefit from a decline in interest rates (and corresponding increase in value of your asset) beyond the strike price of call option and similarly your benefits are capped if the issuer prepays
  
• there is less security to your cash flows because your issuer may pay back the principal thereby stopping coupon payments
  
• All of this will likely happen when interest rates are low and your opportunities to reinvest will be in a low interest market

LOS 61i - Identify the factors that affect the reinvestment risk of a security and explain why prepayable amortising securities expose investors to greater reinvestment risk than nonamortising securities

NB lower coupon increases (duration) interest rate risk but decrease reinvestment risk (since your return was lower to begin with) ceteris paribus

A security has more reinvestment risk when:

• coupon is higher so that interest cash flows are higher
  
• call feature is present
  
• it is amortising
  
• it contains a prepayment option (this also adds risk/uncertainty)

because with each you may be stuck with your principal and no more cash flows at a time when interest rates are low and investment opportunities suck.

LOS 61j - Describe the various forms of credit risk and describe the meaning and role of credit risk

rating indicates probability of default so lower rated bonds have more default risk

difference between yield on Treasuries and lower rated bond of similar maturity is credit spread

yield on a risky bond = yield on a default free bond + credit spread

Credit Spread Risk = default risk premium required in market can increase even when there is no change in similar Treasuries; increase in credit spread risk decreases value of the bond

Downgrade Risk = risk of rating downgrade which would increase required return and decrease price

Bonds issued by the same company may have different ratings depending on capital and priority of bondholder's claims

S&P's ratings:

• AAA = least risk
  
• AAA through BBB- are investment grade
  
• BB and below are speculative (junk bonds or high yield bonds)
  
• D are currently in default

LOS 61k - Explain liquidity risk and why it might be important to investors even if the expect to hold a security to the maturity date

Investors prefer more liquidity to less; low liquidity decreases the number of buyers for my asset so I must sell at a lower (possibly discount) rate

bid-ask spread is an indication of liquidity - highly liquid assets have a very low bid-ask spread

low liquidity = high liquidity risk

• even if you are holding to maturity, liquidity can still be an issue when you have to mark to market at lower price because of decrease in liquidity/widening of bid-ask spread
  
• MTM is done for portfolio performance reporting
  
• MTM also affect repurchase agreements to ensure that collateral value is adequate to support the funds being borrowed; lower valuation = higher cost of funds and decreasing portfolio returns
  

LOS 61l - Describe the exchange rate risk an investor faces when a bond makes payments in foreign currency

• Exchange-rate risk e.g. foreigner investing in T-bills will risk relative value of home currency to dollar

LOS 61m - Explain Inflation Risk

• Inflation Risk - uncertainty about future purchasing power of cash flows

LOS 61n - Explain how yield volatility affects the price of a bond with an embedded option and how changes in volatility affect the value of a callable bond and a putable bond

Without any volatility in interest rates, call provision and put provision have little value ceteris paribus.

• value of a callable bond = value of option-free bond - value of embedded call option
  
• value of a putable bond = value of option-free bond + value of embedded put option


• the value of either option is increased by an increase in yield volatility but look at the formulas to determine effect on the bond price
  
• since the call is subtracted from the value of the bond and the put is added (better for investor), yield volatility will decrease value of callable bond and increase value of putable bond


• fluctation in interest rates affects these in opposite ways


• volatility risk for callable bonds is risk that interest rate volatility will increas


• volatility risk for putable bonds is risk that interest rate volatility will decrease

LOD 61o - Describe the various forms of event risk

Event risk = something significant happening to a company or market segment e.g

• disasters impair the ability of corporation to meet debt obligations if disaster reduces cash flow
  
• corporate restructurings [spin-offs, leveraged buy outs, mergers]may affect cash flows, value of collateral assets, etc.
  
• regulatory issues e.g. clean air requirements may reduce cash available to bondholders and result in downgrade

Problem Set Issues

• if you know the duration and the change in yield then multiple the change in yield by the duration (to get the new duration?) and multiple this by the price.
• e.g. a bond with a 7.3% has a duration of 5.4 and is trading at $985. If yield decreases to 7.1%, the new bond price is -5.4*(-0.2) = 1.08%. New price is 1.0108 * 985 = $995.64
• the value of an embedded put option is the difference between the price of the putable bond and the price of the straight bond (not the face value of the bond)
• zero coupon bond will have the greatest duration and therefore subject to greatest interest rate risk
• Treasury bond pays semi-annual coupon and therefore has reinvestment risk
• AAA bonds can lose their AAA rating and therefore have downgrade risk
• Bond with a call feature has volatility risk even when call cannot be exercised immediately
  

READING 62

Caution:

• Remember for TIPS the coupon is fixed (divide by 2 for semi-annual) but the face value upon which the coupon is based fluctuates based on the inflation rate. For $100,000 worth of TIPS trading at par with a 4% coupon and annula inflation rate at 2.5% what is the inflation adjusted principal value of the bond after 6 months.
  
• It pays the product of the par value, half the coupon, and half the inflation rate so:


• coupon payment = ($100,000 * 1.0125) * (0.04/2) = $2025

Measuring Return With Yield
Coupon is not yield. Yield is essentially your return based as a ratio of the value of the bond. Yield is a figure that shows the return you get on a bond. The simplest version of yield is calculated using the following formula: yield = coupon amount/price. When you buy a bond at par, yield is equal to the interest rate. When the price changes, so does the yield.

Why is yield inversely related to price?
Let's demonstrate this with an example. If you buy a bond with a 10% coupon at its $1,000 par value, the yield is 10% ($100/$1,000). Pretty simple stuff. But if the price goes down to $800, then the yield goes up to 12.5%. This happens because you are getting the same guaranteed $100 on an asset that is worth $800 ($100/$800). Conversely, if the bond goes up in price to $1,200, the yield shrinks to 8.33% ($100/$1,200).

Yield to maturity (YTM)
YTM is a more advanced yield calculation that shows the total return you will receive if you hold the bond to maturity. It equals all the interest payments you will receive (and assumes that you will reinvest the interest payment at the same rate as the current yield on the bond) plus any gain (if you purchased at a discount) or loss (if you purchased at a premium). The key point here is that YTM is more accurate and enables you to compare bonds with different maturities and coupons.

If you are a bond buyer, you want high yields. A buyer wants to pay $800 for the $1,000 bond, which gives the bond a high yield of 12.5%. On the other hand, if you already own a bond, you've locked in your interest rate, so you hope the price of the bond goes up. This way you can cash out by selling your bond in the future.

When interest rates rise, the prices of bonds in the market fall, thereby raising the yield of the older bonds and bringing them into line with newer bonds being issued with higher coupons. When interest rates fall, the prices of bonds in the market rise, thereby lowering the yield of the older bonds and bringing them into line with newer bonds being issued with lower coupons.

Government Bonds
In general, fixed-income securities are classified according to the length of time before maturity. These are the three main categories:

• Bills - debt securities maturing in less than one year.
  
• Notes - debt securities maturing in one to 10 years.
  
• Bonds - debt securities maturing in more than 10 years

READING 63

63e - Computer, compare, and contrast the various yield spread measures

• Yield Spread = Yield on Bond A – Yield on Bond B (doesn't capture interest rate movements if they both move in unison)
  
• Relative Yield Spread =Yield on bond A- Yield on Bond B/ Yield on Bond B
  
• Yield Ratio = Yield on Bond A / Yield on Bond B

Even though the way most investors discuss spreads is based on a Treasury security with the same maturity as the one it is being compared to, an investor can also talk about spreads between any two bonds with the following measures:

1. Absolute Yield Spread
This is the way most spreads are measured in the market. This spread measures the difference in spread between two bonds in terms of basis points.

• Yield Spread = Yield on Bond A – Yield on Bond B

2.Relative Yield Spread
This ratio measures the yield spread relative to the reference bond.

• Relative Yield Spread =Yield on bond A- Yield on Bond B/ Yield on Bond B

3.Yield Ratio
This is just the ratio of the yields between the two bonds.

• The equation is: Yield on Bond A / Yield on Bond B

Market convention is to use the on-the-run government security as the reference yield or bond. So in the above equations, one would replace Bond B with the comparable government security.

Example: Yield Ratios
We want to compare an IBM five-year bond with a yield of 4.5 % and the on- the-run government five-year with a yield of 3.75%

Answer:

• Absolute Yield Spread = 4.5% - 3.75% = .75% or 75 basis points
  
• Relative Yield Spread = 4.5%- 3.75% / 3.75% = .20 = 20%
  
• Yield Ratio = 4.5% / 3.75% = 1.20

Why Relative Spreads Are Better
Investors may find relative spreads a better measure because they measure the magnitude of the yield spread and the way it is affected by interest-rate levels. While absolute spread may be maintained as rates change, relative spreads will move in or out depending on the level of rates.

LOS 63f - Describe a credit spread and discuss the suggested relation between credit spreads and the well-being of the economy

• A credit spread is difference in yields between two issues that are similar in all respects except for credit rating
  
• these spreads show effect of credit quality on yields and reveal risk-return tradeoff investor can expect
  
• during expanding economy, more companies are flush and credit spreads tighten
  
• during contracting economy, credit spreads widen and investors tend toward "flight to quality" such as Treasuries

LOS 63g - Identify how embedded options affect yield spreads

• Yield spreads against a benchmark such as Treasuries will be greater for a callable bond than a similar non-callable bond to compensate the bondholder for reinvestment risk


• Similarly, mortgage passthrough securities which have a prepayment option will have higher yield spreads to compensate boldholder for reinvestment risk
  
• Putable options will have lower yield spreads than otherwise similar option free bonds to compensate issuer for risk of having the bonds sold back to them
  
• important b/c this tells us that spreads for bonds with embedded options are not purely premiums for credit risk, liquidity differences, and maturity (duration) risk

LOS 63h - Explain how the liquidity or issue size of a bond affects its yield spread relative to risk free securities and relative to other securities

• Bonds that have less liquidity have higher spreads
  
• Larger issues tend to be more liquid
  
• Issues with greater size tend to be more liquid and tend therefore to have lower yield spreads

LOS 63i - Computer the after-tax yield of a taxable security and the tax-equivalent yield of a tax-exempt security

• After-tax yield = taxable yield * (1 - marginal tax rate)

Tax exempt securities can offer lower yields due to the tax savings. to compare between taxable and non-taxable yields, use the taxable equivalent yield i.e. the yield an investor must make on a taxable bond to have the same after tax return they would on a tax exempt issue (rearrange the after tax yield formula).

• taxable-equivalent yield = tax-free yield/(1-marginal tax rate)

LOS 63j - define LIBOR and explain its importance to funded investors who borrow short term

• London Interbank Offered Rate - the most important reference rate for floating-rate debt securities and short term lending
  
• A funded investor is borrowing at LIBOR + x to fund investments; his profits depend on his ability to earn more than LIBOR + x

READING 64

If the discount rate is higher than the coupon rate the PV will be less than par. If the discount rate is lower than the coupon rate, the PV will be higher than par value.

How Does a Bond’s Price Change as it Approaches its Maturity Date?
As a bond moves closer to its maturity date, its price will move closer to par. The break down on the three scenarios is as follows:

1.If a bond is at a premium, the price will decline over time towards its par value.
2.If a bond is at a discount, the price will increase over time towards its par value
3.If a bond is at par, its price will remain the same

watch out for:
confusing yield price with coupon payment percentage
read carefully for semi-annual versus annual

LOS 65a - Explain the sources of return from investing in a bond

1. coupon interest payments


2. recovery of principal


3. income from reinvesting the periodic coupon payments

LOS 65b - Computer and interpret the traditional yield measures for fixed-rate bonds and explain their limitations and assumptions

1. current yield expresses only bond's annual interest income - ignores capital gains/losses or investment income:

• current yield = annual cash coupon payment/bond price

2. yield to maturity = annualised IRR based on price and promised cash flows. For bond with semiannual coupon payments, YTM is stated as two times the semiannual IRR implied by the bond's price. The formula that relates the bond price (including accrued interest) to YTM for semi-annual coupon is:

[insert clearer version of bond price formula]
bond price = (CPN1/(1+YTM/2)) + (CPN2/(1+YTM/2)²)+...+(CPN_2N+PAR/(1+YTM/2)^2N)

where:
bond price = full price including accrued interest
CPNt = the semi-annual coupon payment rec'd after t periods
N = number of years to maturity
YTM = Yield to Maturity

YTM and price give the same information i.e. given YTM you can calc. price and given price you can calc. YTM (but not easily in the latter case)

To compute YTM compute as if you were calculating IRR remembering:

• first cash flow is negative and is the bond price


• payments are usually semi-annual so divide coupon payment by two and


• double the number of periods (minus one payment)


• final payment is PAR + semi-annual coupon payment


• multiply the final figure by 2 to get the annual payment

or calculate as if it were an annuity:

• PMT = semi-annual coupon


• PV = neg. bond price


• FV = PAR value


• N = 2 * number of years


• CPT I/Y = semi-annual YTM (so multiply by two)

YTM will be the discount rate you will use to find the price i.e. the YTM/2 will be the discount rate to discount the semi-annual cash flows and the recovered principal to get the bond's price.

if price = par then coupon rate = current yield = YTM

if price <>

if price > par then coupon rate > current yield > YTM

bond equivalent yield = semi-annual pay YTM's (mult. by two to get annual pay YTM). This is the discount rate using semi-annual interest, double the periods, etc. If you were to calculate it on annual interest and annual payments it would just be called the annual pay YTM

the bond equivalent yield is the non-compounded annual rate received from a security that pays semi-annually with only simple interest. So to get an annual pay rate from a BEY you would to:

1. get the semi-annual payment rate (so divide by two)
2. then compound the semi-annual payment rate over two periods

example: what is the annual-pay yield for a bond with a BEY of 5.6%?
answer: [(1+(0.056/2))²-1

BEY/semi-annual pay YTM example: for a semi-annual pay bond, you can calculate the YTM if you know price (PV), par value (FV), number of years (N*2) and then CPT the I/Y and multiply by two i.e. you are trying to find the semi-annual discount rate that would make $1000 become the current price of $768

to find the annual pay YTM you would use the same above except number of years would just be N and not N*2 (gives a slightly higher number obviously). This is the number that would make $1000 become the current price of $768 when discounted annually instead of semi-annually

Yield To Call simply substitutes the call price for the par value and the number of periods until the call date is substituted for the number of periods until maturity

Yield to First Call simple subsitutes the call price for the par value and the number of periods until the first call date is subbed for the number of periods until maturity

Yield to Worst is the worst outcome of all possible provisions of the bond, so find worst case scenario (e.g. Yield to First Call) and calculate; usually the first date on which the money is repaid in some form (e.g. call, refunding, repayment)

Yield to Refunding is same calc as YTM or YTC but here the YTRefunding would use the call price but the date is the date when refunding protection ends

Yield to Put is used for bonds with embedded puts which are selling at a discount. Yield would likely be higher than YTM (advantage investor). The YTP calc is just like YTM but number of semi-annual periods until put date is N and put price is FV

NB Don't forget to:

• N = ensure this multiplied by 2 or kept whole as appropriate
• PMT = ensure divided by 2 or kept whole as appropriate
• I/Y = don't forget to multiple by two as appropriate
• take it easy when you input the numbers, the time will pay off

NB Bonds trading at a discount to par value, YTC will be higher than YTM; bond yields quoted on a yield to call basis when the YTC is less than the YTM which can only be the case for bonds trading at a premium to the call price

Cash Flow Yield (CFY) is used for mortgage backed securities and other amortising asset-backed securities. Amount of principal repayment can be greater than the amount required to amortise the loan over its life. Once cash flows are projected, calculate CFY as a monthly IRR based on the market price of the security.

Primary LIMITATION of YTM is that it does not consider the rate of return we might receive on the reinvested coupon payments i.e. assumes that everything appreciates at the same rate (YTM) whereas in real life the investor might reinvest the coupon payments in a riskier, higher yielding security and may not hold the bond until maturity.

The realised yield is usually computed at the end of the investment horizon (when all the reinvestment rates are known) and captures the reinvestment rate of the coupon payments. If the coupons are invested at a rate equal to YTM then the YTM = realised yield

LOS 65c - Explain the importance of reinvestment income in generating the yield computed at the time of purchase, calculate the amount of income needed to generate that yield and discuss factors that affect reinvestment risk

• The realised yield will always be between the YTM and the (assumed) reinvestment rate


• Once we calculate the total amount needed for a particular level of compound return over a bond's life, we can subtract the principal and coupon payments to determine the amoutn of reinvestment income necessary to achieve the target yield.

So, to calculate the required reinvestment income needed to get a compound return of X:
1. calculate the FV of the par based on the required rate of return
2. subtract the principal payment (plus any discount/premium from par) plus the coupon payments e.g. 180.61 - 100 - 60 = $20.61

LOS 65d - Compute and interpret the BEY of an annual pay bond and the annual pay yield of a semi-annual pay bond

i.e. turn a semi-annual return into an annual return and vice versa

• BEY = [ (1+ annual pay YTM)^1/2 -1] * 2


• EAY = (1+ semi-annual pay YTM/2)² -1

NB must nail down relationship between BEY and YTM. BEY converts annual YTM to what it would be at semi-annual compounding and allows for the comparisons with semi-annual compounding securities. EAY does the opposite i.e. "converts" a semi-annual paying YTM to annualised so it can be compared to annual paying securities.

LOS 65e - Describe the methodology for computing the theoretical Treasury spot rate curve and compute the value of a bond using spot rates

1. begin with the 6 month spot rate


2. set the value of the 1 year bond equal to the present value of the cash flows with the 1 year spot rate divided by 2 as the only unknown


3. solve for the 1 year spot rate


4. use the 6 month and 1 year spot rates and equate the present value of the cash flows of the 1.5 year bond equal to its price, with teh 1.5 year spot rate as the only unknown


5. solve for the 1.5 year spot rate

Valuing a bond using spot rates

sum the discounted value for each of the cash flows at the appropriate rate/2 and number of periods e.g. for the second coupon payment, discount it at the 1 yr spot rate/2; the final payment (at 1.5 years) would be the discounted value of final payment plus the coupon rate using the spot rate for 1.5 years divided by 2 and the number of periods would be 3

LOS 65f - Differentiate between the nominal spread, the zero-volatility spread and the option-adjusted spread

nominal spread = YTM for bond minus YTM for Treasury of similar maturity
nominal spread suffers from same limitations as YTM and ignores the shape of the spot curve (assumes it is flat)

zero-volatility spread = in order to value a bond correctly, we have to increase each of the Treasury spot rates by some equal amount so that the PV of the risky bond's cash flows discounted at the (increased) spot rates equals the market value of the bond.

• use trial and error to solve this.


• Discount each of the cash flows by the spot rate plus some fixed estimated amount until you hit the amount that will discount the cash flows such that they equal the price of the bond


• NB the nominal spread assumes the spot rate curve is flat, therefore, if the spot rate curve is upward sloping, the zero volatility spread (which is based on the spot rate curve) will be higher than the nominal spread and if it is downward sloping the zero volatility spread will be lower than the nominal spread


• NB similarly, if the bond is amortising such as an MBS the diff. between the nominal and the zero volatility spread will be higher than regular bond; also, the earlier the principal is paid off, the greater the difference between the two spread measures

the option adjusted spread (OAS) This is a measurement tool for evaluating price differences between similar products with different embedded options.

• A larger OAS implies a greater return for greater risks. This measure removes the effect of options or prepayment on the spread and allows for comparison between products.


• The OAS is the spread for non-option characteristics such as credit risk, liquidity risk, and interest rate risk.

LOS 65g - Describe how the option-adjusted spread accounts for the option cost in a bond with an embedded option

• option cost in percent = Z-spread - OAS


• A callable bond: option cost > 0 (investor is compensated) and OAS > Z-spread


• A puttable bond: option cost <>
  

LOS 65h - Explain a forward rate and compute spot rates from forward rates, forward rates from spot rates, and the value of a bond using forward rates

Borrowing for X years at the Xyear rate should cost the same as borrowing for 1 yr periods, X years in succession. So the spot rate for 3 years will be the same as the geometric mean of the three separate forward rates.

uses forward rate notation such that _xf_y is the forward rate for an x year loan to be made y years from now so...

1. (1+S₃)³ = (1 + ₁f₀)(1+₁f₁)(1+₁f₂) for finding a forward rate three periods from now


2. S₃ = [(1 + ₁f₀)(1 + ₁f₁)(1 + ₁f₂)]^1/3 - 1 for finding a spot rate equivalent to forwards for three periods

The latter is familiar - it is the geometric mean b/c you are finding the single return that creates the same PV of the cash flows as the single rate in the X year loan.

A spot rate for a maturity of N periods is the geometric mean of forward rates over N periods. The same relation can be used to solve for a forward rate given spot rates for two different periods.

To find a forward rate from a spot rate use the first formula and isolate the unknown on one side of the equation e.g. say we know the spot rate for a two year bond is 8% and we know the current 1 period spot rate is 4% then we can calulate the missing 2nd year forward rate using (1+0.08)² = (1 + 0.04)(1+₁f₁) minus one
divide both sides by 1.04 to isolate the unknown:

• (1.08)²/1.04 = (1+₁f₁) and we get 1.1664/1.04
• or 1.12154 = 1+ 1f1 = 1.12154-1 = 12.154%

why do we want to do this? to know whether it is better to buy the one period bond or the two period bond. In this case, we know buying a one year bond for 4% and a forward rate one year bond for one year from now at 12.154% is better than buying one 2 year 8% bond

multiple years calculation

if you know the 1, 2 and 3 yr spot rates, you can back out to the 1 yr forward and the 2 yr forward. in the above example, we found the 2 yr foward rate. if we know the 3 yr spot rate is 12% we can do the same thing again except using cube of the three year equal to the product of the known one year forward rates (including the unknown):

(1.12)³ = (1.04)(1.12154)(1 + x)
1.4049/(1.04)(1.12154) = 1 + x
1.4049/1.1664 = 1+x
1.2045-1= x
20.45% = x

Quick and dirty way = is to use a simple average of the spot rates to solve for the forward rate; may come close enough to answer the question

Calculate price of T-note using spot rates use the appropriate spot rate for each cash flow to discount the cash flow over the appropriate number of periods e.g. a cash flow of $20 in the second period when the spot rate is 5% would be N=2, I/Y = 2.5, FV=$20, CPT PV

Calculate implied forward rates for loans for more than one period given spot rates of: 1 yr = 5%, 2 yr = 6%, 3 yr = 7% and 4 yr = 8% we can calculate the implied rate on a two year loan two years from now by:

[(1+S4)⁴/(1+S2)²]^1/2-1 = [1.08⁴/1.06²]^1/2-1 = 10.04%

i.e. raise the larger year spot rate to the power of the number of years in the future and divide by the smaller of the years raised to the power of the number of year in the future and then take the x root where x is the duration of the loan in years

Computing a bond value using forward rates

Discount each cash flow by the relevant periods and sum them together. e.g. if one of the cash flows takes place two years from now, discount it by the two year forward rate and then again by the one year current rate.

So if 1 yr rate is 4%, 2 yr forward is 5% and 3 yr forward is 6% and we want to find the value of a 3yr 5% coupon bond with face value of $1000 then we do the following:

(50/1.04) + (50/(1.04)(1.05)) + (1050/(1.04)(1.05)(1.06)) = $1000.98

READING 66

Please let me get to the end of these books... it's scary to think how relieved i will be when all i am doing is revising instead of learning. There is so much i feel i don't have a handle on right now.

full valuation or scenario analysis approach to measuring interest rate risk is based on applying the valuation techniques we have learned for a given change in the yield curve. for more complex bonds, a pricing model incorporating yield volatility as well as specific yield curve change scenarios is required to use full valuation approach. if valuation model is sufficiently good, this is the theoretically preferred approach

duration/convexity approach provides approximationof the actual interest rate sensitivity of a bond or bond portfolio -- for parallel shifts in the yield curve

bond characteristics on duration (price sensitivity)

• higher coupon = lower duration (and vice versa)


• longer maturity means higher duration (and vice versa)


• higher market yield = lower duration (and vice versa)

all of these relations are intuitive if you stop to think about it instead of just memorizing them. If my bond is paying me a lot of money in coupons, I'm less concerned about my ability to invest elsewhere and there will be strong demand for my bond. The longer my bond has to maturity, the more sensitive it will be to interest rate changes because you will be locked into the bond for a longer period and if prices change for the worse, you are stuck with an asset that is no longer as attractive relatively. The shorter the maturity, the closer I am to collecting money and the less uncertainty I have about my assets value. if interest rates go down, I will shortly be able to take advantage of them. the higher my market yield, the lower my sensitivity to interest rate changes for similar arguments advanced above about high coupons.

positive convexity
wow. that term sounds like you're smart when it's actually a pretty simple concept:

• yield and prices for bonds are negatively correlated so yield curve is downward sloping


• this inverse relationship is not a simple straight line but a curve bending toward the origin


• the shape shape of this curve determines the severity of a change in price/yield at each level


• the positive convexity will mean that as yields increase, price decreases at a decreasing rate i.e. prices rise faster than they fall for a given change in yield down or up which is a good thing for a bondholder


• for price-yield relationship to be convex, the slope (rate of decrease) of the curve must be decreasing (level out) as move from left to right


• duration = slope of price-yield curve at any given point

Callable Bonds, Prepayable Securities, and Negative Convexity
All of these securities come with enhanced risk/uncertainty for the bondholder because at certain points, the security could be essentially redeemed/paid off and the bondholder has to find a place to reinvest the money (reinvestment risk).

upside price appreciation is limited (price compression) because as interest rates go down, debtors will be more likely to pay off principal and issuers will more likely call the bond in when it hits the call price (so they can refund for a better rate on their debt)

so for callable bonds the curve bulges out on the left hand side up to the call price, so as yields decrease the price increases at a decreasing rate (which makes sense - lower demand as we approach call price) or negative convexity... as move to the right along the curve, the curve returns to positive convexity

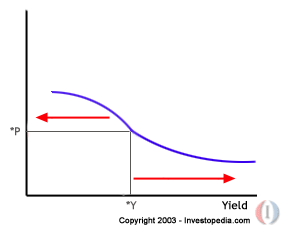
• In the above diagram, the *P price is the call price and the yield that matches the call price is *Y


• The curve for yields below *Y will exhibit negative convexity and will eventually flatten out as we approach the call price *P


• Price volatility for lower yields will naturally be lower for a callable bond than an option free bond (more certainty with callable bond around that price-yield area)


• The curve for yields above *Y will exhibit positive convexity


• MBS or similar securities with prepayment risk will exhibit similar behaviour and therefore have greater reinvestment risk, especially as yields fall

Price volatility characteristics of putable bonds

• Less price volatility at higher yields because as the yield rises, price falls and the put becomes more valuable


• Put option is of no value when price is above the putable price and it behaves just like an option free bond

NB all of this information about convexity implies that i should be able to determine whether a bond has call (or prepayment) or a put depending on the % change in price up or down relative to a parallel shift up or down in yield... but it is difficult because an option free bond would still have a price which drops slower than it rises. I guess it would depend where i am on the curve.

Effective Duration

• remember: duration is ratio of % change in price/% change in yield
  
• given convexity, we know price increases faster when rates fall x than price decreases when they rise x

• effective duration uses the average of the price changes in response to equal increases and decreases in yield to account for this fact


• if we have a callable bond trading in the area of negative convexity, the price increase is smaller than the price decrease but using the average still makes sense
• formula effective yield =

(bond price when yields fall - bond price when yields rise)
2*(initial price)*(change in yield in decimal form)

or average price change (difference between the bond prices divided by 2) divided by current price (so it is now average price as a percentage of current price) and then divided by the change in yield in decimal form (to get change in price as a percentage of current price expressed as a precentage of the change in yield)

Looking at the formula step by step helps me remember it. Much watch my fat fingered mistakes on the calculator.

NB if the question shows a parallel yield shift of 50 bps e.g. current rate is 10% and we want to know the price change at 9.5% and 10.5% then the change in yield will be 50 bps or 0.005% because this is the swing either side

Also helpful:

• price increase in response to the 0.005 decrease above would be PYieldDown-InitialPrice/InitialPrice


• price decrease in response to the 0.005 increase above would be PYieldUp-InitialPrice/InitialPrice

The average of the percentage price increase and the percentage price decrease.
If the change in yield was 50 bps, we can find the duration by multiplying the price change by two to get the percent change in price for a 1% change in yield.

Using effective duration
Once you have your effective duration (e.g. -2.5) for say a bond when yield increases by 50bps, you can calculate the new up or down price by:

• percent change in bond price = - effective duration x change in yield in percent
• or -2.5 * 0.005 = 0.0125 = 1.25%
• so if the bond were priced at $100, it would now be worth $98.75

Other types of duration...

Macaulay duration = estimate of bond's interest rate sensitivity based on the time in years until the promised cash flows will arrive; because Macaulay duration is based on the expected cash flows for an option free bond, it is not an appropriate estimate of the price sensitivity of bonds with embedded options

Modified duration = derived from Macaulay duration and is slight improvement b/c it takes the current YTM into account; also based on expected cash flows for option free bond so not good for bonds with embedded options

Effective duration is the most appropriate measure of interest rate risk for bonds with embedded options because effective duration is calculated from expected price changes in response to changes in yield that explicitly take into account a bond's option provisions (i.e. they are the price-yield function used).

Interpreting Duration

1. duration is the slope of the price-yield curve at the bond's current YTM
2. (Macaulay) duration is a weighted average of the time (in years) until each cash flow will be received; the weights are in proportions of the total bond that each cash flow represents
3. duration is the approx. change in price for a 1% change in yield (price sensitivity to a change in yield)

Duration of a portfolio is just the weighted (by market value i.e. market price * par value e.g. 102 * 1,000,000 means 102% of 1,000,000 or 1,020,000) average of the individual bonds within the portfolio

duration is a good measure of the sensitivity of portfolio value to parallel shifts in the yield curve; changes to the shape of the yield curve may affect different securities differently and this will not be captured in the portfolio duration

convexity is a measure of the curvature of the price-yield curve; a straight line has a convexity of zero

duration assumes the price-yield curve is zero (ignores changes in shape) and will underestimate the price of the bond (except when curve is flat)

A bond's approximate percentage price change based on duration and convexity
Combining duration and convexity gives us more of a full picture and a more accurate estimate of the % change in price of a bond - esp. for large changes in yield

percentage change in price = duration effect + convexity effect

= {[-duration * change Y] + [convexity * (changeY)²]} * 100

with changeY entered as a decimal, the *100 is necessary to see it as a percentage

watch out: the duration will be negative when yield rises and positive when yield falls so percentage change in price will be different for a rise than for a fall i.e. will not both rise and fall by x. Say duration is -2% (yield has risen) and convexity is 8% then total change will be 6% but if yield falls and duration is +2% then total change will be 10% (2+8)

when convexity is negative (e.g. low yields cause negative convexity for callable bonds) the convexity adjustment to the duration-only based estimate of the percentage change will be negative for both yield increases and decreases

Effective Convexity takes into account changes in cash flows due to embedded options while modified convexity does not and therefore effective convexity is the appropriate measure for bonds with embedded options just as effective duration is appropriate for measuring bonds with embedded options instead of modified duration

Price value of a basis point (PVBP) is the dollar change in the price/value of a bond or portfolio when the yield changes by one basis point or 0.01%

PVBP = duration * 0.0001 * bond value

This is actually a little more complicated than it looks. Don't forget that semi-annual effective durations will need to be multiplied by 2 to get annualised version. if you want to know the difference in price. It is actually:

PVBP = initial price - price if yield changes by 1bp

calculate the duration (e.g. 5%) and add one basis point (5.01) and redo the calculation using this new rate and then find the difference between the two prices.