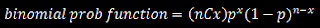Study Session 3 - Reading 12 Technical Analysis

LOS 12a. explain the underlying assumptions of technical analysis;

Technical analysts believe in the following:

• that history repeats itself, so look for trends
• trends persist over an appreciable length of time
• value and prices are determined by supply and demand
• causes are difficult to determine but shifts in supply/demand reveal themselves in market pirce behaviour

Efficient Market Hypothesis (EMH) analysts are opposed and believe:

• market prices follow a random (unpredictable) walk
• new information gets immediately priced in
• that technicians are wasting their time; too subjective and looking for past trends that never reoccur the same way

Fundamentalists are more in the technical camp but they believe that causes for price behaviour can be observed through analysing earnings and publicly available data - that the economic fundamentals such as return vs. risk determine market prices

• Technicians look for a price move; expect price move to happen fairly quickly as new data is observed and processed by the market
• Fundamentalists look for why the price will move; expect price move to happen slowly
• EMH analysts that when price shifts happen, the happen rapidly - instant digesting of new information by the market

LOS 12b. discuss the advantages of and challenges to technical analysis;

Technical analysis pros:

• quick/easy
• no accounting data needed
• incorporates pyschological and economic reasons
• tells you when to buy (but not why)

Technical analysis cons:

• too subjective
• historical relationships may not be repeated
• EMH belief that models cannot predict random price walk
• technical trading rules would be self-fulfilling
• if successful, trading rules would be copied and erase the arbitrage

LOS 12c. list and describe examples of each major category of technical trading rules and indicators.

Four classes of technical trading rules/indicators:

1. contrarian = opposite of what majority is doing
2. smart money followers = buy when smart money buys, sell when it sells
3. momentum indicators = when market moves in a direction, buy/sell with it
4. price-and-volume = look for significant corresponding movements in both price and volume and act accordingly

Contrarian Opinion Rules

• Cash position of mutual funds if mutual fund cash ratio (mut.fund cash/total assets) is high(>11%) then funds are bearish (so contrarians buy). If low (<4%)>
• Investor credit balances in brokerage accounts Falling credit balances mean normal investors are bullish and buying (so contrarians sell)
• Opinions of investment advisory services if bearish sentiments index is high (>60%) then contrarians buy.
• OTC vs. NYSE volume OTC are more speculative. A high ratio of OTC to NYSE means normal investors are bullish (so contrarians sell).
• CBOE put/call ratios If ratio is high (>0.6) then most normal investors are trying to sell, so contrarians buy. Low (<0.4)>
• Stock index futures When future traders are bullish (>70%) then contrarians sell.

Smart money rules

three indicators:

1. Confidence Index (CI) by Barrons = ratio of yields on high grade bonds to yields on broader (riskier) bonds. So if CI is high, investors are confident and are selling high grade bonds to buy better earning lower grade bonds. If CI is up, smart money investors are buying.
2. TED - T-Bill/eurodollar yield spread - spreads widen during crisis, flight to Treasuries. Smart money is bearish.
3. Debit balances in brokerage accounts (margin debt) - if margin debt is high, smart money is buying (bullish).

Momentum indicators

Breadth of market

• indices represent a few, large companies
• market has many medium/small companies
• index may go one way while smaller issues go the other way
• comparing advance-decline line and index - if they move together, then there is a broad market movement

Stocks above their 200 day moving average

• if over 80% of stocks trade above their 200 day avg then the market is overbought (therefore bearish). if 20% are above 200 day avg then market is oversold (therefore bullish)

Stock Price and Volume Techniques

• Dow Theory = stock prices move in trends: major trends, intermediate trends, short-run movement. Technicians look for reversals and recoveries in major market trends

• Volume price changes on high volume tell us whether suppliers or demanders are driving change.
• upside/downside volume ratio = vol. of stocks that increased/vol. of stocks that declined
• If ratio is 1.75 or more, market is overbought (bearish). If less than 0.75 then market is oversold (bullish)

• Support/resistence levels most stock prices are stable; fluctations up hit resistence, flux down receives support
• Moving average line trends again. Random flux masks trends. By using moving averages (10 to 200 days) true trends will appears amongst the noise of randomness
• Relative strength = stock price/market index value i.e. is a stock outperforming the market (positive trend) or underperforming relative to market

Study Session 3 - Reading 11 Hypothesis Testing

LOS 11a. define a hypothesis, describe the steps of hypothesis testing, interpret and discuss the choice of the null hypothesis and alternative hypothesis, and distinguish between one-tailed and two-tailed tests of hypotheses;

• hypotheses is a statement about the value of a pop parameter developed for the purpose of testing a theory or belief
  1. state hypothesis
  2. choose test statistic e.g. mean
  3. choose level of significance
  4. state decision rule
  5. collect sample/calculate sample statistics
  6. decision on hypothesis
  7. investment decision
• null hypothesis H₀ is the thing you want to reject and is usually what it would mean to end up outside the confidence interval and might be x = 5 or x > 6
• alternative hypothesis H_a is the thing you want to "prove"
• use one tailed for greater than or less than
• use two tailed for equalities
• most are two tailed

OK. I found this a little confusing - usually my problem was that I couldn't quite figure out what I was proving at the end of it all. Must focus on a good rejection rule and applying it well. I'm going to spend some time here and include an example from Schweser because I found this confusing when I read it:

Example (two tailed):
We have data on daily returns on a portfolio of call options over 250 day period. The mean daily return has been 0.1% (0.001) and the sample standard deviation of portfolio returns is 0.25% (0.0025). researcher beleives that the mean daily return is not equal to zero (so our hypothesis is that it is equal to zero):

1. Ho: μ= 0, Ha: μ ≠ 0

Since this is an equality, use two tailed test for mean (#2). At 5% significance, we look up standard deviations in z table for 95% which is ±1.96 (#3). So we can come up with our decision rule:

4. Reject Ho if +1.96 <>

5. Calc. statistic by standardising the test statistic by dividing test stat (mean) by the standard error. This will convert it into standard deviations which we can then compare against our rule. So 0.001/standard error where standard error is 0.0025/sq.rt. 250 and we get 0.001/0.000158 = 6.33

6. Look back at decision rule in #4 and since 6.33 > 1.96 we reject null hypothesis.

7. We can conclude that the mean return is significantly different from zero given sample's standard deviation and size i.e. the two values are different from one another after considering the variation in the sample

Common error - i tend to misread 0.25% as 25 percent instead of 0.0025 etc.

LOS 11b. define and interpret a test statistic, a Type I and a Type II error, and a significance level, and explain how significance levels are used in hypothesis testing;
Hypothesis testing involved two statistics: the test statistic calculated from the sample and the critical value of the test stat

• The test statistic is the difference between the sample stat (e.g. sample mean) and the
• hypothesized stat (the one stated in the null hyp.), divided by the standard error
• Type I error: rejection of null when it is actually true
• Type II error: Failure to reject null when it is actually false
• significance level α is the probability of a Type I error e.g. sig. level = 5% /95% confid.

LOS 11c. define and interpret a decision rule and the power of a test, and explain the relation between confidence intervals and hypothesis tests;

• Decision rule is to reject or fail to reject null
• decision is based on distribution of the test stat
• typical decision rule: if test stat is (greater/less than) the value X, reject the null
• power of a test is the prob of correctly rejecting null when it is false
• power of test is all about rejecting; if you incorrectly reject then P = α, if you correctly reject then power of test = 1-P e.g. 95%
• For any α, you can only descrease the prob of Type II (and increase power of test) by increasing sample size

Confidence Intervals and Hypothesis Tests

• confidence levels are about comparing in actual units rather than standard deviations
• [sample stat-(crit. value)(stand. error)]≤ pop parameter ≤ [sample stat.+(crit. value)(stand. error)]
• this is intuitive: the pop parameter lies in a range of values depending on confidence interval. So if standard error is 0.0158 and sample mean is 0.1 and we want to be 95% confident, we mult. 1.96 (dev's for 95% prob) by the standard error and get 0.030968 which is the percentage deviation from the mean. So we know the pop parameter lies somewhere in the range of 0.1 ± 0.030968

LOS 11d. distinguish between a statistical result and an economically meaningful result;
This concept is basic. Even though you may get a statistically positive return, transaction costs may make erase/diminish it so your investment decision must take this into account

LOS 11e. explain and interpret the p-value as it relates to hypothesis testing;

• p-value is prob of obtaining a test stat that would lead to rejection of null when it is actually true (type I)
• It is the bit leftover in the tail(s)... so if we find our test stat in the tail past the critical value, the leftover bit(s) is the p-value (in two tailed tests, we sum the leftover bit in each)
• If our test stat is found at 99% (at 95% conf., 2.5% in each tail) we would reject the null but there is still that 1% chance in each tail that we are wrong to do so

LOS 11f. identify the appropriate test statistic and interpret the results for a hypothesis test concerning the population mean of both large and small samples when the population is normally or approximately distributed and the variance is 1) known or 2) unknown;

• Rule of thumb: when in doubt use t statistic
• Use t-test if pop variance is unknown and either small sample but normal or large sample
• As we said earlier, small sample and unknown variance with nonnormal means we can't rely on the answer at all
• calculate t stat as before in hyp testing i.e. diff between sample stat and hyp stat divided by standard error
• the z stat and the t stat are calculated the same way except the t stat includes the degrees of freedom to derive the probability/deviations
• 
  

Critical Z values - important!

two tailed test significance levels and corresponding critical z values

• 0.10 is ± 1.65
• 0.05 is ± 1.96
• 0.01 is ± 2.58

one tailed test

• 0.10 is +1.28 or -1.28
• 0.05 is +1.65 or -1.65
• 0.01 is + 2.33 or -2.33

LOS 11g. identify the appropriate test statistic and interpret the results for a hypothesis test concerning the equality of the population means of two at least approximately normally distributed populations, based on independent random samples with 1) equal or 2) unequal assumed variances;

I sort of skimmed this because the formula is ridiculous but the summary is this:

• for two independent samples from two normally dist. pop's, the different in means can be tested (to see if it equals zero i.e. they are the same number) with a z-stat
• if variances are assumed equal the denominator is based on the variance of the pooled samples
• when variances are assumed unequal, denominator is based on combination of the two samples' variance
• otherwise testing of the hypo is done the same way once you have your result i.e. does it lie within or outside the chosen prob range

LOS 11h. identify the appropriate test statistic and interpret the results for a hypothesis test concerning the mean difference of two normally distributed populations (paired comparisons test);

• paired comparisons are done when the variables being tested are dependent in some way but the sample distributions are still normal
• A t-stat is used in this case
• t = avg difference of the n paired observations from hyp value/sample standard error

LOS 11i. identify the appropriate test statistic and interpret the results for a hypothesis test concerning 1) the variance of a normally distributed population, and 2) the equality of the variances of two normally distributed populations, based on two independent random samples;

Chi Square test of variances (normal distribution)

• Chi square test is used for hyp tests concerning variance of normally distributed populations i.e. if i believe the variance to be a, my Ho: x ≠ a
• chi-squared distribution is asymmetrical and approaches normal as df increases
• looks lognormal i.e. bounded by zero, humped to the left
• different prob in left tail than right tail - Chi-squared table captures this and is used by matching the df with the prob in the appropriate tail (NB divide sig level by two for two tailed tests)
• Chi squared formula = (df * s²)/σ² _hyp
• i.e. degrees of freedom mult by sample variance, divided by hypothesized variance

F-test for equality of variances of two normally distributed pops (independent random samples)

• F-test is just variance2/variance1
• Ratio of the variance in question with the larger one on top
• Use F-table to support or reject hypothesis (match degrees of freedom for each sample - numerator df is on the top of the table)
• rejection region is in the right side of the table
• if you are looking at the difference in divergence/dispersion of earnings between two industries, use greater than in rule

LOS 11j. distinguish between parametric and nonparametric tests and describe the situations in which the use of nonparametric tests may be appropriate.

• parametric tests rely on assumptions regarding distribution of population and are specific to pop parameters (hence the name)
• non-parametric tests either do not consider a particular pop parameter or have few assumptions about the population that is sample
• non-parametric tests are used when there is concern about quantities other than the parameters of a distribution or when the assumptions of parametric tests cannot be supported e.g. ranked observations

Study Session 3 - Reading 10 Sampling and Estimation

LOS 10a. define simple random sampling, sampling error, and a sampling distribution, and interpret sampling error;

• simple random sampling: every item has an equal chance of being selected
• can be done by assigning a number to each item and using random numbers to select or by systematically choosing every nth item
• sampling error = the difference between the sample stat (e.g. mean) and the corresponding population parameter (e.g. pop mean) i.e. how (un)representative is the sample stat
• sampling distribution of the sample stat is probability distribution of all possible sample stats from a set of equal sized samples randomly drawn from same population

LOS 10b. distinguish between simple random and stratified random sampling;

• simple random is just random or systematic sampling
• stratified random sampling is proportionate - ensuring that the random sample contains a representative number of observations from each category e.g. different stocks

LOS 10c. distinguish between time-series and cross-sectional data;

• time-series is looking at one category across multiple time periods
• cross-sectional is looking at multiple categories during one single time period

LOS 10d. interpret the central limit theorem and describe its importance;

• central limit theorem states that for a large enough sample size n (usually > 30) from a pop with a mean μ and a variance σ², the prob distribution for the sample mean will be approx. normal with a mean μ and a variance of σ²/n
• Theory allows us to use normal distribution to test hypotheses about pop mean, regardless of distrib. of the pop
• As the sample size grows, the sample stats become closer to the pop parameters
• The sample mean will be approximately normally distributed.
• The sample mean will be equal to the population mean (μ).
• The sample variance will be equal to the population variance (σ2) divided by the size of the sample (n)
• Thus the central limit theorem can help make probability estimates for a sample of a non-normal population (e.g. skewed, lognormal), based on the fact that the sample mean for large sample sizes will be a normal distribution.

LOS 10e. calculate and interpret the standard error of the sample mean;

• standard error is the standard deviation (of the pop or, if not available, the sample) divided by the square root of the sample size
• the sample mean and standard error can be used to calculate approximate confidence intervals for the mean i.e. the actual pop mean will lie between a and b with 95% confidence

LOS 10f. distinguish between a point estimate and a confidence interval estimate of a population parameter;

• point estimate is a single sample value used to estimate pop parameters e.g. sample mean representing the pop mean where sample mean is a point estimate of the pop mean
• confidence interval gives a range of values within which the actual value of a parameter will lie, given a probability of 1 - α (α is the level of significance)

LOS 10g. identify and describe the desirable properties of an estimator;

• unbiased = the expected value of the estimator is equal to parameter you are trying to estimate
• efficient = variance of sampling distribution is smaller than all other unbiased estimators
• consistent = as sample size grows, estimator accurace increases i.e. standard error decreases

LOS 10h. explain the construction of confidence intervals;

• confidence intervals are the point estimate ± (reliability factor * standard error)

LOS 10i. describe the properties of Student’s t-distribution and calculate and interpret its degrees of freedom;

• Student's t-distribution is used when sample size is <>
• It results in more conservative confidence intervals (curve is platykurtic - fat tails)
• t-distribution is symetrical
• defines by degrees of freedom (df) calculated by n-1 (sample size minus one)
• t distribution converges to z distribution as sample size (degrees of freedom) becomes sufficiently large

LOS 10j. calculate and interpret a confidence interval for a population mean, given a normal distribution with 1) a known population variance, 2) an unknown
population variance, or 3) an unknown variance and a large sample size;

• here we are trying to calculate the probability of the pop mean being within a certain range of values based on the sample mean distribution
• when available, use population parameters to calculate the confidence interval
• the calculation for when distribution is normal with known variance is:
• 
  where x is the sample mean,
  z_α/2 is the reliability factor i.e. the z-score that leaves α/2 in the upper tail,
  e.g. z_α/2 = 1.65 for 90% confidence (sig. level is 10% i.e. 5% in each tail) - might want to just think of this as 10% instead of thinking about the tails bit
  and the last part is the standard error

So for example, you have a sample mean test score of 80% with a standard error of 5 at 95% confidence, then the true pop mean would be between 75% and 85% with 95% confidence

• when variance is unknown, use t distribution:
• 
• here the t_α/2 part is the t-statistic corresponding to a t-distributed random variable with n-1 degrees of freedom

Rules of thumb for when to use t or z

• if distribution is non-normal then small sample sizes do not work
• if normal w/ known pop variance then use z statistic
• if normal w/ unknown variance use t statistic
• non-normals only work with large samples, use z or t depending on whether you know variance

LOS 10k. discuss the issues regarding selection of the appropriate sample size, data-mining bias, sample selection bias, survivorship bias, look-ahead bias, and time-period bias.

• data mining = overestimating significance of a pattern in a data set; test pattern on out of sample data to confirm or deny overestimation of significance
• sample selection bias = systematic exclusion of data from analysis, usually because unavailable (creates non-random samples)
• survivorship bias = exclusion of samples such as using only surviving mutual funds in sample
• look-ahead bias = basing the test at a point in time on data not available at that time
• time-period bias = relation does not hold over other time periods

Study Session 3 - Reading 9 Common Probability Distributions

LOS 9a: Explain a probability distribution and distinguish between discrete and continous random variables

• A probability distribution is the probabilities of all possible outcomes for a random variable.
• Discrete random variables are finite and countable (e.g. number of days on which it rained) whereas a continuous random variable can be an infinite number (e.g. rainfall for each day - the possible outcomes between 1 and 2 inches is infinite 1.00001, 1.0002, etc.) and is described as ranges instead (e.g. prob. that rainfall will be between 1 and 2 inches or, say, less than 1 inch).

LOS 9b: Describe the set of possible outcomes of a specified discrete random variable

• For discrete distribution p(x)=0 when it cannot occur and p(x) > 0 when it can.
• p(x) means the prob that rand. variable X=x
• For continous distribution p(x)=0 even though x can occur (because x cannot be a single value) so only p(x1 <>
• For price changes, generally use continuos e.g. prob. that price will be between $1 and $2
  

LOS 9c: Interpret a probability function, a probability density function, and a cumulative distribution function

• Probability function p(x) is the prob. that a rand. variable = a specific value.
• Two key properties:
  • 0 ≤ p(x)≤ 1
  • Sum of p(x) = 1 ... this makes sense since the sum of all probabilities should be 1
• Both the PDF and the CDF are cumulative functions
• A probability density function (or pdf) describes a probability function in the case of a continuous random variable. Also known as simply the “density”, a probability density function is denoted by “f(x)”. Since a pdf refers to a continuous random variable, its probabilities would be expressed as ranges of variables rather than probabilities assigned to individual values as is done for a discrete variable. For example, if a stock has a 20% chance of a negative return, the pdf in its simplest terms could be expressed as:
• A cumulative distribution function (cdf) is constructed by summing up, or cumulating all values in the probability function that are less than or equal to x and is very similar to the cum. freq. except for probabilities. May be expressed as F(x) = P(x ≤ x)

LOS 9d: Calculate and interpret probabilities for a random variable, given its cumulative distribution function
Take a prob. function for X={1,2,3,4], p(x) = x/10 which means that for the set of the whole numbers 1,2,3,4 the probability of each is 10%, therefore, f(3) is 0.6 which is the sum of 1/10, 2/10 and 3/10 i.e. the cumulative probabilities of all numbers up to and including the number in question. Same process if the prob's are different for each outcome.

LOS 9e: Define a discrete uniform random variable and a binomial random variable

• The above function is a discrete uniform random variable i.e. the prob. of each number occuring is equal i.e. for x={a,b,c] the p(a)=p(b)=p(c)
• The prob. for a range of outcomes is p(x)k where k is the number of possible outcomes in a range
• binomial random variable is the number of "successes" given a number of trials where the outcome is binary ("success" or "failure"). Might be used for the probability of a stock moving up once to $4.55 (the "success" is the up move might be duu where the d and u cancel) after n periods (the number of trials).
• Definition of "success" is crucial to this working out.

LOS 9f: Calculate and interpret probabilities given the discrete uniform and the binomial distribution functions

In English, this says multiply the number of combinations that you could have x successes out of n trials by the proportionate prob of success and by the proportionate prob of failure.

Expected value of X for Binomial Random Variable
For a given series of n trials, the expected value is n * p
i.e. if we perform n trials and the prob. of success on each trial is p we expect np successes.

LOS 9g: Construct a binomial tree to describe stock price movement
this is fairly straightforward. Remember: If the up movement is 1.05 it means the price increases by 5% so mult. 1.05 by the stock price. the down movement will be the reciprocal 1/1.05.

LOS 9h: Describe the continuous uniform distribution and calculate and interpret probabilities, given a continuous uniform probability distribution

• A continuous uniform distribution describes a range of outcomes, usually bound with an upper and lower limit (say a and b), where any point in the range is a possibility.
• Since it is a range, there are infinite possibilities within the range. In addition, all outcomes are all equally likely (i.e. they are spread uniformly throughout the range).
• To calculate probabilities, find the area under a pdf curve.
• Basically, take the range between a and b is 100% of the prob. so the 100 divided by all the values between a and b gives you the prob. for each. Sum the number of values in the range you are looking for and mult. them by the prob. of each.
• Technically, this is achieved by the following: P(x1 ≤ X ≤ x2) = (x2-x1)/(b-a) where x1 to x2 is the value range you are looking for and b to a is the range of all values.

LOS 9i: Explain the key properties of the normal distribution, distinguish between a univariate and a multivariate distribution, and explain the role of correlation in the multivariate normal distribution

Normal distribution has following properties:

• completely described by mean and variance
• skewness = 0 and kurtosis = 3
• the tails are asymptotic
• 90% = 1.65
• 95% = 1.96
• 99% = 2.58

Univariate = distribution of one variable

Multivariate distribution

• is dist. of more than one variable and is meangingful only when the variables are dependent on one another.
• If the return of each variable is normally dist. then the distribution of the portfolio will be normal as well.
• Want a low correlation among your portfolio assets.
• 0.5n(n-1) will tell you the number of variances and means you need to describe mult. distribution

LOS 9j: Determine the probability that a normally distributed random variable lies inside a given confidence interval
if μ is $1 and σ is 5% we can say that 66% of the time, the expected return will be ± 5% (one σ) or between $0.95 and $1.05. So the confidence intervals for this example will be:

• 66% = x±1σ
• 90% = x±1.65σ
• 95% = x±1.97σ
• 90% = x±2.58σ

LOS 9k: Define the standard normal distribution, explain how to standardise a random variable, and calculate and interpret probabilities using the standard normal distribution

Standardise translates the value into a number of standard deviations so it can be compared to confidence intervals and a probability determined. This is called the z-value and is the diff. between the observation and the mean divided by the standard deviation or:

A z value of +1 would mean that the obs is one standard deviation above the mean, a z value of -1 means it falls one standard deviation below the mean.

Calculating Prob's using z-values
Standardise the value and then look up the appropriate prob. in the z-table.

• NB watch out for greater than or less than since the z-table is cumulative.
• If your z-value is 1.65 and you want to know prob of outcome being less than x then prob. is 90% since 90% of outcomes fall below x.
• If you want to know prob of outcome being more than x then prob is 1-0.90 or 10% because this is the small bit that isn't covered in the 90%

LOS 9l: Define shortfall risk, calculate the safety first ratio, and select an optimal portfolio using Roy's safety first criterion

• Shortfall risk is focus on both risk and return as opposed to simply the return
• 
• Maximise SFR i.e. just like with Sharpe ratios, you want the highest SFR possible as it gives you the best prob. of returns greater than threshold.

LOS 9m: Explain the relationship between normal and lognormal distributions and why the lognormal distribution is used to model asset prices

• Normal dist. are bilaterally symmetric and can take on any value
• lognormal is always greater than zero and skews to the right
• lognormal is generated by e^x and natural log (ln) of e^x is x
• lognormal for asset prices because they cannot be negative
• lognormal for modeling price relatives i.e. end of period divided by begin price

LOS 9n: Distinguish between discretely and continuously compounded rates of return and interpret a continuously compounded rate of return, given a specific holding period

• use discrete (normal) compounding for interest that compounds during specific times
• use continuous (lognormal) compounding for continous
• Annual rate (continuous) is ln(1+HPR) or rate of return[2nd][e^x]-1 e.g. if portfolio returned 20% then continuous compounding is found by ln 1.20
• Get return from annual rate (or holding period return) by reversing it i.e. 1+annual rate [ln]

LOS 9o: Explain Monte Carlo simulation and historical simulation and describe their major applications and limitations

Monte Carlo

• allows for "what if?"
• can simulate many possible variables and situations
• complex but is only as good as the underlying assumptions

Historical simulation

• based on historical data but past performance does not guarantee future results
• does not allow "what if?" scenarios
  
  

Study Session 2 - Reading 8 Probability Concepts

LOS 8a - Define a random variable, an outcome, an event, mutually exclusive events, and exhaustive events
These are fairly intuitive, so I'll just deal with the last two:

• mutually exclusive = cannot both happen at the same time
• exhaustive = includes all possible outcomes (probabilities will sum to 1)

LOS 8b - Explain the two defining properties of probability and distinguish among empirical, subjective and a priori probabilities

• Probability is always between 0 and 1
• Sum of probabilities of mutually exhaustive and mutually exclusive events will be 1.
  
• empirical probability is established through analysis of past data
• a priori probability is deduced or uses logic e.g. 5 out of 10 stocks yesterday were up therefore a random stock from this ten had a 50% probability of going up
• subjective = educated guess

LOS 8c - State the probability of an event in terms of odds for or against the event

• Here I rely on how i hear this in regular speech. e.g. if the odds are 9 to 1 against an event, I know there is a good chance (90%) that this will not occur.
• Only tricky part is remember that the above would not be 10 to 1. e.g. if probability of an event happening is 20% then the odds in favour are 1 to 4 and the odds against are 4 to 1.

LOS 8d- Distinguish between unconditional and conditional probabilities

• Unconditional = prob of an event regardless of past or future occurrence of other events
• Conditional = occurrence of one event affects the probability of the occurrence of another event

LOS 8d - Define and Explain the multiplication, addition, and total probability rules

• mult. rule = P(AB) = P(AB) * P(B) i.e. prob of A and B taking place where A is dependent on B
• addition rule = P(A or B) = P(A) + P(B) - P(AB) i.e. prob of A or B taking place is the sum of their probabilities minus the prob of both taking place (to avoid double counting). NB don't forget to subtract the overlap
• total prob = P(AB₁)P(B₁) + P(AB₂)P(B₂) +...+ P(AB_n)P(B_n)

LOS 8f: Calculate and interpret (1) the joint probability of two events, (2) the probability that at least one of two events will occur, given a probability of each and the joint probability of two events, and (3) a joint probability of any number of independent events

1. joint probability of two events A,B is calc. using mult. rule P(AB) = P(AB)*P(B)
2. if the events are independent, then P(AB) = P(A) so joint prob is P(AB) = P(A)*P(B)
3. prob. of at least one of two events occuring is addition: P(A or B) = P(A)+P(B)-P(AB)

LOS 8g: Distinguish between dependent and independent events

This is fairly intuitive. Events A and B are independent IFF:
P(AB) = P(A) or vice versa, P(BA) = P(B)
otherwise they are dependent

LOS 8h: Calculate and interpret, using the total probability rule, an unconditional probability

The total probability (unconditional probability) of an event R is calc.:

P(R) = P(RS₁) * P(S₁) + P(RS₂) * P(S₂) +...+ P(RS_n) * P(S_n) where the set of events {S₁), S₂),...S_n)} is mutually exclusive and exhaustive

This is also fairly intuitive in a real world setting. Say you are trying to find the total probability of a rise in interest rates given the state of the economy:

P(Poor Economy) = 0.30
P(Interest Rates Rising Poor Economy) = 0.10
P(Normal Economy) = 0.50
P(Interest Rates Rising Normal Economy) = 0.40
P(Good Economy) = 0.20
P(Interest Rates Rising Good Economy) = 0.70

The total probability is the sum of the joint probability for each event i.e.
(0.30)(0.10)+(0.50)(0.40)+(0.20)(0.70) = 0.03+0.20+0.14 = 0.51 or 51% probability

Note: This will often be structured as a tree diagram which is a good way to visualise it if they do not present it this way and helps visual people like me "get it"

Expected Value

The degree of dispersion of outcomes around an expected value of a random variable is measured using the variance and standard deviation

When pairs of random variables are being observed, the covariance and correlation are used to measure the extent of the relationship between the observed values for the two variables from one obs to the next

The Expected Value is the weighted average of all the possible outcomes of a random variable (e.g. interest rate rise) where the weights are the probabilities that the outcome will occur. Again this is fairly intuitive: it is the sum of the final node results in the tree diagram:

E(X) = P(x1)x1 + P(x2)x2 + ... + P(xn)xn

NB when all probabilities are equally likely, the E(X) is simply the arithmetic mean

LOS 8i: Explain the use of conditional expectation in investment applications

Just like the interest rates example above, conditional expected values are contingent upon the outcome of some other event (e.g. state of the economy). Conditional expected value would be revised using Bayes' formula when new information arrives.

LOS 8j: Diagram an investment problem using a tree diagram

This is a visual representation of the kind of problem shown above. Say a stock price moves with the state of the economy (up or down). We would have four cases:

1. good economy, stock up
2. good economy, stock down
3. bad economy, stock up
4. bad economy, stock down

As in the example with interest rates, each comes with its own probability (e.g. prob. of a good economy and then corresponding prob. of stock going up and prob. of stock going down)

**********Must update this to include tree diagram***********

LOS 8k: Calculate and interpret covariance and correlation

Cov(Ra,Rb) = Sum of Prob(x) * (dev from mean for A for scenario x)(dev from mean for B for scenario x)

So this is calculated in four steps:

1. calculate expected return for A and B
2. calculate deviations from expected return for A and B for each scenario
3. multiply the deviations for A and B for each scenario and then multiply the product by the probability for that scenario
4. sum the resulting products

Correlation
Correlation is an easier to interpret measure of the same relationship between A and B and is found by:

Correlation(A,B) = Cov(A,B)/σA * σB

Correlation properties:
ranges from -1 to +1 (perfect negative correlation to perfect positive correlation with zero being no correlation)

LOS 8l: Calculate and interpret the expected value, variance and standard deviation of a random variable and of returns on a portfolio

Portfolio expected value = weighted average of the assets (or returns)

Portfolio variance took me a while to process because it looks scarier than it actually is. It is simply a way of taking the sum of the weighted variances of each asset's return and the weighted covariance of the assets' returns. So for assets A and B the formula is:

Var(Rp) = w_A²σ_A² + w_B²σ_B² + 2w_Aw_Bσ_Aσ_BCorr(A,B)

• Note: σ_Aσ_BCorr(A,B) is the covariance(A,B) so if you are not given the Corr, you can find it for the first half of the formula and then substitute the Cov(A,B) after the weights in the second half. Also, this is for a portfolio of only two stocks.
• For more stocks, the number of the weighted variances increases by the number of stocks and the number of Cov increases such that all possible pairings of stocks are considered.

LOS 8n: Calculate and interpret an updated probability using Bayes' formula

Well, this one really messed me up. As usual, it was simpler than I assumed by looking at the formula. The definition for the formula is:

updated probability = (prob. of new info for given event/uncond. prob. of new info)*prior prob. of event

This didn't make sense to me because i couldn't tell what the new info was and what the unconditional info was etc.

The way I do it is by thinking of the tree diagram. If we diagram out the possibilities for a stock rising or falling given different probabilities for different states of the economy and then we are told that the stock did rise and we are asked for the probability that the economy was good as a result then my formula would be:

updated probability = probability that stock rose and econ was good/total prob. of economy being good

That is the resulting prob at the end of the node where the stock rose and the econ was good divided by the sum of the resulting probabilities at the end of all the nodes where the econ was good.

Bayes tells us the updated probability now that we know the "answer" to the original question i.e. that the stock rose

LOS 8o: Identify the most appropriate method to solve a particular counting problem and solve counting problems using the factorial, combination and permutation notations

The way this was described was confusing but the bottom line is that you are trying to figure out how many options there are to assigning a set of data to different groups such as if you were trying to assign employees to different development teams.

• If the number of groups is the same as the number of people then use n! (n[2nd][x!])
• If the number of groups is not the same and order is not important then n [2nd][nCr] r where n is the total number and r is the number of groups n!/(n-r)!r!
• If the number of groups is not the same and order is important then n [2nd][nPr]r where n is the total number and r is the number of groups n!/(n-r)!

Study Session 2 - Reading 7 Statistical Concepts and Market Returns

LOS 7a - Descriptive vs. Inferential Statistics
Descriptive allow one to analyse and summarise large data sets - turns data into information.
Inferential involves making forecasts, estimates/judgments about a larger group from samples and is founded on probability theory.

Nominal Ordinal Interval Ratio

LOS 7b - Frequency Distribution

1. Define the intervals - must be exhaustive and not overlap
2. Assign the observations to their relevant intervals
3. Count the observations
   

LOS 7c - Relative Frequency, Cumulative Frequency

• Absolute frequency = the # of observations in each interval (e.g. 2, 3, 5)
• Relative frequency = % of observations in each interval (e.g. 20%, 30%, 50%)
• Cum. Abs. Freq. = the cumulative # of obs in each interval (e.g. 2, 5, 10)
• Cum. Rel. Freq. = the cum frequency in each interval (e.g. 20%, 50%, 100%)

LOS 7d - Histograms

Graphical representation (either bar or polygon) of frequency distribution. Intervals on x, absolute (usually) frequency on y axis.

LOS 7e - Define, calculate and interpet measures of central tendency, including the population mean, sample mean, arithmetic mean, weighted average or mean, geometric mean, harmonic mean, and mode

All of these are essentially measures of expected returns w/r/t to stocks or portfolios with the exception of harmonic mean which is used largely in dollar cost averaging.

population/sample mean = is simply the arithmetic mean of all the observations and will often be used as Expected Value or Expected Return when referring to stock prices or returns. Sum of all deviations from mean will equal zero.

weighted mean/average is used where the observations have unequal influence on the mean. Multiply the values by their weights and then sum them all. Often used to find Expected Return of a portfolio where different stocks have different weights in portfolio so their returns are averaged using weighted average.

Note: The weighted average in many guises is used in other formulas where values are averaged but they are not equal e.g. variance of a portfolio where stocks have different weights.

median - midpoint. Middle observation. If there are an even number of observations, the median is the average of the middle two observations.

geometric mean is often used when calculating investment returns over multiple periods or when measuring compound growth rates. To calculate, take the nth root of the product of the n observations:






The first is the general formula for geometric mean. The second is used for calculating returns (which is quite a common use).

harmonic mean used for dollar cost averaging. divide the number of obs by the reciprocals of the obs, so...






harmonic mean <>

LOS 7f - Quartiles and other 'iles
These are just intervals. Divide the range by the appropriate number (5 for quintiles, 100 for percentiles) to get the size of the intervals. Remember, no overlapping.

To locate the position of the observation at a given percentile, y, with n data points sorted in ascending order (e.g. find the observation located at the 30th percentile):

LOS 7g - Define, calculate, and interpret 1) a range a mean absolute deviation and 2) the variance and standard deviation of a population and of a sample

• Range = (max value - min value)
• mean absolute deviation = average of the absolute value of all deviations from the mean.
• population/sample variance = measures volatility/risk and is the square root of the average of the squared deviations from the mean. The average can be found arithmetically or using a weighted average as appropriate to the problem.

standard deviation is the most common expression of risk and is simply the square root of the variance. The σ is useful because it is expressed in the same units as the observations i.e. if your observations are in $ and cents then so is your σ.

LOS 7h - Calculate and interpret the proportion of observations falling within a specified number of standard deviations of the mean using Chebyshev's inequality

Chebyshev's inequality tells you the % of obs that lie within k standard deviations of mean is at least 1-1/k²

Works for any distribution and tells you minimum % and gives the following key markers:

• 36% = +-1.25 standard deviations of the mean
• 56% = +-1.50 standard deviations of the mean
• 75% = +-2 standard deviations of the mean

LOS 7i - Define, calculate, and interpret the coefficient of variation and the Sharpe ratio

Coefficient of variation is a measure of dispersion in a distribution relative to the mean and allows us to make direct comparison of dispersion across different sets of data. Allows us to measure risk (variability) per unit of expected return whereas Sharpe measures return per unit of risk.

CV = standard deviation of x/average value of x

Sharpe Ratio measures excess return per unit of risk and is the risk premium divided by the standard deviation. Portfolios with large Sharpe ratios are preferred because they give more return per unit of risk. To calculate:

Very similar to Safety First Ratio.

LOS 7j - Define and interpret skewness, explain the meaning of a positively or negatively skewed return distribution and describe the relative locations of the mean, median, and mode for a nonsymmetrical distribution

OK. Skew is just like we use it in common speech. If we say that will skew the results it means throw them off in one direction or another. Positive skew says that there are positive outliers and so the distribution is humped to the left. Negative is humped to the right with a long left tail of negative possibilities.

• Positive skew = mean > median > mode
• Negative skew = mean <>
• For a symmetrical distribution, they are equal.

NB put the three measures in alphabetical order and arrows point in the direction of skew.

LOS 7k - Define and interpret measures of sample skewness and kurtosis

• kurtosis measures peakness of distribution and normal dist. = 3
• leptokurtic is more peaked, mesokurtic is normal and platykurtic is less peaked than normal
• lept = leap, meso = same, plat = flat

To calculate skew:

Note: skew is cubed which allows for a positive or negative results. The formula for kurtosis is the same formula but to the fourth power instead of cubed. Excess kurtosis is result minus 3.

To calculate kurtosis:

LOS 7l: Discuss the use of arithmetic mean or geometric mean when determining investment returns

• use geometric mean for measures of past performance over multiple years/periods as it gives us the compounded rate
• use arithmetic mean as estimator of next year's returns

Notes on Study Session 3

• Don't forget that sample mean is still found by dividing by total number of observations but the variance/standard deviation is divided by n-1
• Semivariance and semideviations are covered in the CFAI books but not in Schweser
• You are asked to calculate semivariance, semideviations, kurtosis and skew in CFAI books but not in Schweser (although the principles and concepts of kurtosis and skew are covered by Schweser)
• Semivariance and semideviation are just calculating the variance and the st. deviation using only the data below the mean - otherwise it is exactly the same. You will still use the sample mean and the sample total number of observations but you only sum the squares of the observations below the mean
• don't forget to check whether to divide by n or n-1 i.e. pop or sample
• modal interval is the interval with the most number of observations in it
• Geometric mean always screws me up because i keep doing some approximation of the standard deviation formula:
  Geometric mean = (((1+R₁)(1+R₂)...(1+Rn))^1/n)-1